약분계산기 및 약분하는 방법과 연습문제

약분 계산기

약분을 하는 분수의 분모·분자를 계산기에 입력하고 「계산하기」 버튼을 누르면 약분을 계산하는 계산기입니다.

약분 이란

분모와 분자가 다른 2개의 분수라도 분모와 분자가 같은 수를 곱한 분수(혹은 같은 수를 나눈 분수) 이면 같은 분수가 됩니다.

분수를 이미지로 해 보면 알기 쉬운데요. 아래 그림을 보면 분모와 분자가 다른 분수에서도 같은 의미라는 것을 알 수 있습니다.

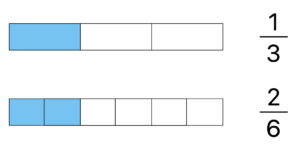
또 분수를 소수로 변환해 봐도 같은 의미의 분수라고 하는 것을 알 수 있습니다. 분수는 분자를 분모로 나누어 소수로 바꿀 수 있습니다.

이 분수의 성질을 이용하여 분모 분자를 같은 수로 나누어 분모와 분자를 최소의 분수로 하는 것을 약분 이라고 합니다.

약분하는 방법

우선 약분을 하는 기본적인 방법은, 분모·분자를 같은 수로 나누어 더 이상 나눌 수 없게 될 때까지 반복하는 방법이 있습니다.

이 방법은 나눗셈을 할 수 있으면 할 수 있는 약분의 방법입니다. 다만 분모·분자의 수가 크면 나누는 횟수도 많아져 계산이 힘들어지는 경우도 있습니다.

약분을 하는 또 다른 방법으로서 분모와 분자의 최대 공약수를 구하고, 그 최대 공약수로 분모·분자를 나누면 한번에 약분을 할 수 있습니다.

분모와 분자의 최대 공약수를 구할 수 있으면 간단하게 약분을 행할 수 있습니다.

최대 공약수에 대한 내용;

최대공약수 계산기 및 계산방법과 예문

최대공약수 계산기 최대공약수를 구하고 싶은 숫자를 입력하고 계산하기 버튼을 누르면 최대공약수를 계산해 줍니다. 최대공약수의 의미와 계산방법 그리고 예문도 소개하고 있으니 참고해 주세요. (adsbygoogle = w...

calc.wikibest.co

2023.10.15

약분으로 분모가 1이 되면 정수로

약분하면 분모가 1이 될 수도 있습니다. 분모가 1이면 정수와 동일하므로 정수로 쓰도록 합니다.

분모나 분자가 소수인 경우의 약분

분모나 분자가 소수인 경우는 정수로 다시 약분을 행합니다. 예를 들어 0.3이라면 10을 곱하고, 0.03이라면 100을 곱하는 것처럼 정수가 되도록 곱셈을 합니다. 주의점은 분모와 분자에 같은 수를 곱한다는 것입니다. 분모에만 곱하거나 분자에만 곱하면 다른 의미의 분수가 되어 버리므로 반드시 분모 분자에 같은 수를 곱하도록 합니다.

대분수의 약분

대분수를 분수로 하여 약분해 보면 알 수 있습니다만, 결국 분수 부분만을 약분한 것과 대답은 같기 때문에 분수 부분만을 약분하는 편이 계산을 간단하게 할 수 있습니다.

왜 약분이 필요할까?

같은 의미의 분수라면 왜 약분이 필요한지 생각할지도 모릅니다. 약분을 하는 목적은 주로 두가지가 있습니다.

1. 수의 계산을 할 때 분모와 분자의 수가 크면 계산이 번거롭기 때문에 약분을 행하여 분모와 분자를 최소화하여 계산을 하기 쉬워진다.

2. 대답이 분수인 경우에 약분하여 알기 쉬운 분수로 한다.

약분할 수 있는 분수는 약분까지 한다는 것이 룰입니다. 시험에서 약분까지 하지 않으면 오답이 되는 경우도 있기 때문에 약분 할 수 있는 경우는 반드시 약분을 하는 습관을 붙여 두면 좋다고 생각합니다.

약분 예문

\({10}\over{2}\)을 약분하세요.

\begin{align*}
\frac{10}{2} &= \frac{10÷2}{2÷2} \\
&= \frac{5}{1} \\
&= 5
\end{align*}

\({18}\over{30}\)을 약분하세요.

\begin{align*}
\frac{18}{30} &= \frac{18÷6}{30÷6} \\
&= \frac{3}{5}
\end{align*}

\({24}\over{36}\)을 약분하세요.

\begin{align*}
\frac{24}{36} &= \frac{24÷12}{36÷12} \\
&= \frac{2}{3}
\end{align*}

\({30}\over{40}\)을 약분하세요.

\begin{align*}
\frac{30}{40} &= \frac{30÷10}{40÷10} \\
&= \frac{3}{4}
\end{align*}

\({36}\over{48}\)을 약분하세요.

\begin{align*}
\frac{36}{48} &= \frac{36÷12}{48÷12} \\
&= \frac{3}{4} \\
\end{align*}